introduction
Au cœur de notre vision de la nature se trouvent deux systèmes fascinants: le réseau de neurones dans le cerveau humain et le réseau cosmique de galaxies.
Le cerveau humain est une structure complexe à plusieurs échelles temporelles et spatiales dans laquelle coexistent des phénomènes cellulaires, moléculaires et neuronaux. Il peut être modélisé comme un réseau hiérarchique (c'est-à-dire «le connectome humain» [ 1 ]), dans lequel les neurones se regroupent en circuits, colonnes et différentes zones fonctionnelles interconnectées. La structure du réseau neuronal permet la liaison entre différentes zones, toutes consacrées au traitement d'activités spatio-temporelles spécifiques sur leurs neurones, formant la base physique et biologique de la cognition [par exemple, Réf. 2]. Certains des défis majeurs des neurosciences contemporaines sont de démêler la structure du connectome (par exemple, la carte complète des connexions neuronales dans un cerveau), de comprendre comment cette structure peut produire des fonctions cognitives complexes, et de définir le rôle des cellules gliales et du microenvironnement dans la physiologie interneuronale.
L'Univers, d'après la vaste collection de données de télescope rassemblées pendant plusieurs décennies, semble être raisonnablement bien décrit par un modèle physique «consensuel» appelé le ΛΛModèle CDM (Lambda Cold Dark Matter), qui tient compte de la gravité de la matière ordinaire et sombre (c'est-à-dire des particules en interaction très faible), de l'espace-temps en expansion décrit par la relativité générale, et de l'énergie anti-gravitationnelle associée à l'espace vide , appelée «énergie noire». Un tel modèle donne actuellement la meilleure image de la façon dont les structures cosmiques ont émergé de l'arrière-plan en expansion et ont formé la toile cosmique [par exemple, Réf. 3 et 4]. Les éléments constitutifs les plus importants du réseau cosmique sont les halos dominés par la matière noire auto-gravitante, dans lesquels la matière ordinaire s'est effondrée pour former des galaxies (et toutes les étoiles à l'intérieur). La distribution initiale des fluctuations de densité de matière a été amplifiée au début par l'action de la gravité et s'est développée en groupes ou amas plus grands de galaxies, filaments, feuilles de matière et vides, dans un réseau à grande échelle dans toutes les directions de l'espace. Parmi les principaux défis auxquels la cosmologie est encore confrontée, figurent la nature physique de l'énergie noire, la composition de la matière noire (ou le domaine des scénarios alternatifs pour celle-ci), la tension apparente entre différentes mesures du taux d'expansion de l'Univers, la séquence exacte des processus responsables de la variété de la morphologie des galaxies et de leur co-évolution avec les trous noirs supermassifs [par exemple, Réf.5 , pour une revue récente].
Bien que les interactions physiques pertinentes dans les deux systèmes ci-dessus soient complètement différentes, leur observation par des techniques microscopiques et télescopiques a capturé une morphologie similaire alléchante, au point qu'il a souvent été noté que le réseau cosmique et le réseau de neurones se ressemblent [par exemple. , Réf. 6 et 7 ].
Dans ce travail, nous appliquons des méthodes de la cosmologie, des neurosciences et de l'analyse de réseau pour explorer cette question qui suscite la réflexion de manière quantitative pour la première fois, à notre connaissance.
Matériaux et méthodes
Immunohistochimie et microscopie
Nous avons analysé plusieurs échantillons indépendants de cortex cérébral et cérébelleux humain fixés au formol et inclus en paraffine [ 8 ], échantillonnant des tranches de profondeur4 μ m 4 μm, avec des facteurs de grossissement de 4 ×4×, 10 ×10× et 40 ×40×. Les neurofilaments ont été marqués en utilisant l'anticorps monoclonal de souris Neurofilament (2F11) (Ventana / CellMarque / Roche). Les échantillons ont été automatiquement traités par Ventana BenchMark Ultra Immunostainers. Un microscope Nikon eclipse 50i a ensuite été utilisé pour visualiser les échantillons. Grossissements supérieurs à40 ×40× a été évitée afin d'obtenir une meilleure résolution en profondeur optique, ainsi que pour minimiser la réponse non linéaire de la microscopie optique.
Simulations cosmologiques
Nous avons utilisé des échantillons synthétiques de la toile cosmique d'une haute résolution (2400324003 cellules et particules de matière noire) simulation d'un cube 1003 Mpc31003 Mpc3 volume cosmique (1 Mpc = 3,085 ⋅dix24 cm1 Mpc=3.085⋅1024 cm), réalisée avec le code de réseau ENZO [ 9 ] comme détaillé dans Réf. 10 . La simulation produit une distribution réaliste de la matière noire, de la matière ordinaire et des champs magnétiques à l'époque actuelle. Afin d'imiter la procédure de «tranchage» des tissus cérébraux, nous avons produit 12 tranches minces différentes (d'épaisseur25 Mpc25 Mpc) à partir du volume simulé, en extrayant quatre tranches dans des directions perpendiculaires par rapport à chacun des axes indépendants de la simulation. Nous donnons un accès public à nos images Web cosmiques, ainsi qu'aux échantillons de cerveau et aux images d'autres réseaux naturels discutés ci-dessous à cette URL https://cosmosimfrazza.myfreesites.net/cosmic-web-and-brain-network- ensembles de données .
Résultats
Nombres absolus, proportions internes et composition
Nous citons d'abord les données disponibles dans la littérature, qui nous permettent une première comparaison sommaire des tailles absolues des deux systèmes. Le rayon de l'Univers observable estRU∼ 13,9 GpcRU∼13.9 Gpc[ 11 ]. L'extrapolation d'observations récentes postule qu'un total deNg∼ 2,6 ⋅dix12Ng∼2.6⋅1012les galaxies peuvent être présentes dans la sphère de l'Univers observable [ 12 ], avec jusqu'à∼ 5 ⋅dixdix∼5⋅1010galaxies de masses égales ou supérieures à celle de la Voie lactée. Les plus grands amas de galaxies totalisent une masse dépassantdix151015 masses solaires (1 masse solaire = 1,989 ⋅dix33 g=1.989⋅1033 g). De longs filaments de matière ordinaire et sombre, avec une extension de plusieurs dizaines de mégaparsèques, relient des amas et des groupes de galaxies et sont séparés par un espace principalement vide [par exemple, Réf. 4 ].
Selon des estimations récentes, le cerveau humain adulte contient Nneu≈ 8,6 ± 0,8 ⋅dixdixNneu≈8.6±0.8⋅1010neurones au total, et presque un nombre égal de cellules non neuronales. Seulement~ 20 - 25 %∼20−25% de tous les neurones sont situés dans la matière grise corticale (représentant ∼ 80 %∼80% pourcentage de la masse cérébrale), tandis que le cervelet a environ ∼ 6,9 ⋅dixdix∼6.9⋅1010 neurones (∼ 80 %∼80%des neurones cérébraux) [ 13 , 14 ].
On remarque que les deux systèmes sont organisés en réseaux bien définis, avec ∼dixdix-dix11∼1010−1011 nœuds interconnectés par des filaments (si l'on considère comme nœuds toutes les galaxies de masse comparable ou supérieure à celle de la Voie lactée, voir ci-dessus), dont l'étendue typique n'est qu'une infime fraction (≤dix- 3≤10−3) de la taille de leur système hôte. En outre, les galaxies et les neurones ont un rayon d'échelle typique, qui n'est qu'une très petite fraction de la longueur typique des filaments auxquels ils sont connectés. De plus, les données disponibles suggèrent que le flux d'informations et d'énergie dans les deux réseaux se limite principalement à≤ 25 %≤25% du contenu masse / énergie de chaque système.
Dans le cas de l'Univers, nous nous référons à la composition actuelle, basée sur Planck Collaboration et al. [ 15 ], la distribution d'énergie relative étant fonction du temps dans leΛΛModèle cosmologique MDP; pour le cerveau humain, nous nous sommes référés aux recherches publiées sur la composition du cerveau humain [par exemple, Réf. 16 et 17 ].
En résumé: 1) le cerveau est composé d'eau (77 - 78 %77−78%), lipides (10 - 12 %10−12%), protéines (8 %8%), les glucides (1 %1%), substances organiques solubles (2 %2%), sel (1 %1%); 2) l'Univers est fait pour un73 ∼ %73∼% par Dark Energy (un champ d'énergie scalaire de l'espace vide), pour un 22,5 %22.5% par Dark Matter, pour 4,4 %4.4% par la matière baryonique ordinaire et pour moins de ≤ 0,1 %≤0.1% par les photons et les neutrinos.
De manière frappante, dans les deux cas ∼ 75 %∼75%de la distribution masse / énergie est faite d'un matériau apparemment passif, qui imprègne les deux systèmes et n'a qu'un rôle indirect dans leur structure interne: l'eau dans le cas du cerveau, et l'énergie sombre en cosmologie, qui dans une large mesure ne affectent la dynamique interne des structures cosmiques [par exemple, Réf. 18 ].
Comparaison morphologique
De petits échantillons du cortex cérébral et cérébelleux humain ont été prélevés pendant la corticectomie pour aborder les tumeurs sous-corticales (section 2.1). Les cellules neuronales ont ensuite été colorées avec l'anticorps monoclonal clone 2F11 contre les neurofilaments, qui sont des filaments intermédiaires spécifiques des neurones dans le cytoplasme des neurones qui fournissent un support structurel au cytosquelette neuronal, ainsi que des microtubules et des microfilaments. Il a été montré que le nombre, l'espacement et la densité surfacique des neurofilaments dans les neurones sont des mesures avec une forte dépendance du calibre axonal [par exemple, Refs. 19 - 21 ]. Bien que la densité des microtubules dépende également du calibre des axones, il a été montré que les microtubules forment souvent de petits amas à proximité des organites membraneuses [ 22]. Pour cette raison, nous considérons que les neurofilaments pourraient être disposés de manière plus homogène dans le neurone, et susceptibles d'être une meilleure cible pour visualiser la distribution spatiale des neurones dans les tranches. Pour le réseau cosmique, nous avons analysé chacune des 12 tranches minces du volume simulé (section 2.2), pour évaluer l'effet de la variance cosmique. Une telle approche bidimensionnelle imite ce qui est fait avec des échantillons de cerveau, et en raison du grand degré d'isotropie du réseau cosmique à si grande échelle, cette approche peut également être utilisée pour traduire facilement nos statistiques dans le cas en trois dimensions.
La figure 1 donne un aperçu des détails des structures observées à différentes échelles (à partir de4 ×4×, 10 ×10× et 40 ×40×grossissements dans le cas des tissus cérébraux, et sur les étapes correspondantes en zoom dans le cas du web cosmique) dans notre jeu de données. Surtout à grande échelle, les différents échantillons ne présentent aucun degré de similitude spectaculaire. En particulier, le rôle prédominant des grandes surdensités marquées par des amas de galaxies est évident dans l'échantillon de toile cosmique, tandis que la structure plus fine des neurofilaments dans les échantillons de cerveau produit des modèles à petite échelle plus riches. Au plus fort grossissement atteint dans nos tranches de cerveau, cependant, le réseau raffiné de corps neuronaux et de filaments commence à présenter une certaine similitude avec la toile cosmique sur≤ 20 Mpc≤20 MpcBalance. En se concentrant sur des coupes histologiques, une certaine variabilité peut être remarquée qui dépend de différents sous-types neuronaux dans le cerveau et le cortex cérébelleux. Dans la première tranche, de petits neurones dans la couche granulaire sont représentés, ainsi que la transition vers la couche gangliar avec quelques cellules de Purkinje au bas de l'image. À l'inverse, la deuxième coupe représente de grandes cellules pyramidales entrecoupées de petites cellules neuronales de la matière grise du cerveau (cellules granulaires).

FIGURE 1 . Cartes de contraste de densité normalisé,δρδρpour des exemples de tranches du cervelet (rangée du haut), du cortex cérébral (rangée du milieu) et de la distribution de la matière noire de la toile cosmique (rangée du bas), pour différents niveaux de grossissement. L'analyse spectrale et réseau présentée dans ce travail se concentrera principalement sur40 ×40× échantillons comme dans les panneaux de droite.
Nous utiliserons dans ce travail des outils statistiques pour 1) comparer la distribution de la structure sur toute la gamme du continuum des échelles spatiales de nos échantillons, également par rapport à d'autres systèmes complexes naturels (section 3.3); 2) mesurer les propriétés de connectivité entre les nœuds du réseau, en estimant la tendance à former des configurations fortement groupées (voir la section 3.4).
Analyse spectrale
Nous avons utilisé ici une statistique couramment utilisée en cosmologie: le spectre de puissance de densité, P( k )P(k), qui mesure directement les contributions de différentes fréquences spatiales, k = 2 πL / lk=2πL/l(où l est l'échelle spatiale et L est l'échelle maximale de chaque système), au contraste de densité, défini commeδρ = ρ /ρ¯- 1δρ=ρ/ρ¯−1, où ρ est la densité et ρ¯ρ¯est la densité moyenne de chaque échantillon. Nous mesuronsP( k )P(k) pour nos échantillons bidimensionnels, en décomposant δρδρ en une série de fréquences spatiales discrètes, δ(k→)δ(k→): ⟨ ô(k→) δ(k′→) ⟩ =2π3P( k )δ2ré(k→+k′→)⟨δ(k→)δ(k′→)⟩=2π3P(k)δD2(k→+k′→), où δ2réδD2 est la fonction delta de Dirac bidimensionnelle.
Dans le cas de la simulation cosmologique, ⟨ P ⟩⟨ρ⟩est uniquement contraint par les conditions initiales de la simulation, tandis que dans l'échantillon du cortex et du cervelet, nous le définissons sur la base de la moyenne mesurée dans l'échantillon lui-même. Bien qu'il soit trivial de connaître avec précision le contraste de densité locale dans la simulation, il convient de noter qu'une cartographie précise de l'intensité de pixel enregistrée à une densité de matière projetée est loin d'être triviale en observation au microscope, en raison de la réponse non linéaire de l'imagerie microscopique. processus. Comme indiqué dans la section 2.1, notre choix d'utiliser des échantillons de tissus très fins et un grossissement ne dépassant pas× 40×40est en effet motivé par l'objectif de minimiser la réponse non linéaire de la microscopie optique, en gardant la profondeur optique faible par rapport à l'ouverture de l'image. Pour cette raison,δρδρdans nos échantillons de cerveau est strictement une mesure du contraste des absorptions optiques le long de la ligne de visée, que nous supposons être un proxy pour le contraste de densité dans un souci de comparaison avec des échantillons cosmologiques. Nous avons appliqué la transformation de Fourier rapide standard avec des conditions aux limites périodiques pour calculer les spectres de puissance des échantillons de toile cosmique (car les domaines sont vraiment périodiques), tandis que dans le cas des échantillons de cerveau, nous avons utilisé une technique standard de remplissage à zéro pour incorporer les échantillons observés dans une2 × 22×2une zone plus grande et vide, et une apodisation appliquée aux interfaces entre la zone vide et les données, afin de minimiser les effets de bord parasites, comme cela est couramment fait dans les simulations [par exemple, Réf. 23 ].
Les spectres de puissance résultants sont illustrés à la figure 2 . Il convient de souligner que les spectres de puissance sont libres de glisser horizontalement dans le tracé, en ce sens que l’échelle de référence L relative àk = 1k=1est décidé a-posteriori. Dans ce qui suit, après une comparaison préliminaire des spectres, nous avons ajusté l'échelle horizontale de sorte quek = 1k=1 Correspond à L = 1,6L=1.6 mm dans des échantillons de cerveau, et à L = 100 MpcL=100 Mpcdans le web cosmique. Cela correspond à un rapport d'échelle de1,875 ⋅dix271.875⋅1027entre les deux systèmes. L'amplitude des spectres dans la direction verticale, au contraire, est auto-normalisée à la variance totale deδρδρdans chaque échantillon. En conséquence, les échantillons de cerveau sont normalisés différemment àk = 1k=1, car lorsqu'un grossissement plus faible est utilisé et que des échelles spatiales plus grandes sont échantillonnées, ≤ 1,6≤1.6 les échelles mm contribuent proportionnellement moins à la variance de δρδρdans l'ensemble de l'échantillon. Dans le premier panneau, nous comparons les spectres d'une tranche de toile cosmique aléatoire avec des tranches de cerveau aléatoires obtenues avec différents grossissements. La comparaison montre de façon frappante (en ligne avec ce qui est suggéré sur la figure 1 ) qu'une similitude remarquable avec les spectres est obtenue en comparant≤ 1≤1 échelles mm dans les échantillons de cerveau à ≤ 100≤100Échelles MPC du web cosmique. La plupart des cellules neuronales observées dans nos échantillons cérébelleux sont des cellules granulaires, avec des somata ayant un∼ 5 μ m ∼5 μm diamètre, tandis que leurs dendrites ont des dendrites avec un ∼ 13 μ m ∼13 μmlongueur. La longueur de l'axone (bien que variable selon les aires corticales) est en moyenne de l'ordre de plusieurs millimètres [par exemple, Réf. 24 ]. Considérant que les tranches utilisées pour l'inspection microscopique le plus souvent ne sont pas parallèles à l'axe des axones, il est probable que des fragments de ces fibres autour~ 1 - 2 mm∼1-2 mmen longueur sont visibles dans les tranches. Par conséquent, l'excès de puissance des spectres de puissance neuronale dans ce régime spatial reflète l'abondance de structures avec cette distribution de taille typique.

FIGURE 2 . À gauche: spectres de puissance des fluctuations de densité dans tous les échantillons (dans le cas d'échantillons de cerveau, les spectres de tranches de différentes tailles et facteurs de grossissement sont affichés). À droite: spectres de puissance des fluctuations de densité (dans le cas des tissus cérébraux, seuls les40 ×40×tranches sont utilisées ici), avec des zones ombrées englobant toute la distribution des spectres pour tous les échantillons (12 tranches pour les échantillons de toile cosmique et quatre pour les échantillons de cerveau). Les spectres de puissance de comparaison d'autres systèmes naturels d'échantillons sont représentés par des lignes grises.
En revanche, les fluctuations mesurées sur ≥ 1 - 2≥1-2 Les échelles mm dans les échantillons de cerveau présentent une forme spectrale plus raide que dans les spectres de la toile cosmique. Pour cette raison, dans le reste de l'analyse, nous nous sommes concentrés sur les ensembles de données de40 ×40×échantillons de cerveau pour une comparaison étroite avec des tranches de toile cosmique. Dans le deuxième panneau, nous montronsP( k )P(k) à la fois pour la matière noire et la distribution de gaz de toutes les tranches, qui sont presque identiques à grande échelle (≥≥Mpc) et plus diffus à des échelles plus petites en raison de l'effet de lissage de la pression du gaz. Quant aux spectres de la toile cosmique, nous montrons l'enveloppe contenant tous les spectres de tous40 ×40×échantillons avec des zones ombrées. Nous trouvons un large accord sur près de∼ 2∼2décennies à des échelles spatiales. La similitude entre le cervelet sur0,01 - 1,6 mm0,01-1,6 mm échelles et la distribution de la matière noire de la toile cosmique sur 1 -dix2 Mpc1-dix2 Mpcles écailles sont remarquables. À des échelles plus petites, l'échantillon de cortex affiche beaucoup plus de puissance que le cervelet, en raison de la distribution de petits neurones dans la couche granulaire décrite ci-dessus, tandis que la distribution baryonique de la toile cosmique a moins de puissance, en raison de l'effet (bien connu) de la pression du gaz pour lisser les fluctuations de la densité du gaz baryon à une échelle suffisamment petite pour que les effets hydrodynamiques soient pertinents. Dans tous les cas, nous mesurons des lois de puissance brisées, contrairement à ce qui est attendu pour des distributions fractales (plus simples) [par exemple, Réf. 25 ]. Cela va dans le sens de plusieurs travaux qui ont montré qu'à petite échelle,r ≤ 20 Mpcr≤20 Mpc la fonction de corrélation de la galaxie évolue comme ∝r- 1∝r-1(où r est l'échelle spatiale dans la fonction de corrélation à 2 points) tandis qu'à des échelles plus grandes, la densité ne dépend que faiblement (logarithmiquement) de la taille du système [par exemple, Réf. 26 et 27 ].
Enfin, nous avons produit des spectres de puissance de contrôle pour d'autres échantillons tirés au hasard de réseaux naturels (nuages du ciel, branches d'arbres, turbulence de l'eau et turbulence magnéto-hydrodynamique - tous disponibles sur https://cosmosimfrazza.myfreesites.net/cosmic-web-and- brain-network-datasets ), dans le but de vérifier que notre méthode n'est pas biaisée pour produire une similitude entre des systèmes physiques vraiment différents. Comme le montrent les lignes grises dans le panneau droit de figure 2, de tels systèmes affichent un comportement spectral de loi de puissance plus régulier, clairement en désaccord avec ce que l'on trouve dans les principaux réseaux analysés dans ce travail - même si dans ce dernier cas nous n'avons pas effectué une analyse complète sur toute la plage dynamique de tels systèmes, à la recherche de l'émergence de caractéristiques spectrales possibles comme dans le cas du cerveau et des échantillons cosmiques.
Cependant, les spectres de puissance sont aveugles aux corrélations de phase dans le champ continu, par conséquent deux distributions morphologiquement différentes peuvent encore produire des spectres similaires [ 28 ]. Dans la section suivante, nous nous appuierons donc également sur des méthodes non spectrales pour comparer les différents échantillons.
Analyse de réseau
La science des réseaux a proliféré dans diverses disciplines physiques, y compris les neurosciences [par exemple, Réf. 29 - 32 ] ainsi que la cosmologie [par exemple, Réf. 33 et 34 ]. Une analyse de réseau complexe peut partiellement atténuer le problème de ne pas avoir d'estimateurs de densité parfaitement cohérents dans nos échantillons, en ce sens que la définition des nœuds des différents réseaux est moins sensible aux détails de cartographie exacts des images. Nous nous concentrons ici sur deux paramètres de réseau simples couramment utilisés dans la théorie des graphes et l'analyse de réseau [par exemple, Réf. 35 et 36 ]. Le premier est le degré de centralité,CdCd, qui mesure le degré de connectivité d'un réseau dans la zone localisée (déterminé par une longueur de liaison maximale, llinkllink):
où kjkjest le nombre de connexions (non dirigées) vers / depuis chaque nœud j et n est le nombre total de nœuds dans tout le réseau. Le deuxième paramètre est le coefficient de clustering, C , qui quantifie l'existence d'une structure dans le voisinage local des nœuds, par rapport à un réseau de points aléatoires (c'est-à-dire le rapport des triangles connectés de nœuds à tous les triplets possibles dans un cluster connecté donné) . Il est mesuré comme
dans lequel yjyjest le nombre de liens entre les nœuds voisins du j -node.
Alors que des méthodes sophistiquées pour identifier les nœuds et les filaments dans le réseau cosmique simulé [par exemple, Réf. 4 ] ou dans le réseau neuronal [par exemple, Réf. 37 ] ont été proposées, nous explorons ici une approche plus simple avec l'avantage d'être facilement applicable aux deux réseaux. La méthode est inspirée des procédures standard de «recherche de halo» en cosmologie pour identifier les halos auto-gravitaires dans la toile cosmique [ 38 ]. En détail: 1) nous marquons les pics d'intensité les plus élevés dans toutes les cartes (c'est-à-dire, les pixels en haut10%10%de la distribution d'intensité de chaque carte); 2) nous calculons l'intensité moyenne enfermée des pixels dans des cercles de rayon croissant, jusqu'à une valeur seuil basse,ΔΔ, correspond. Le rayon du cercle atteignant leΔΔ valeur définit le rayon de chaque nœud du réseau (rΔrΔ); 3) tous les pixels à distance≤rΔ≤rΔsont supposés appartenir à ce nœud. Dans le cas du web cosmique, nous avons adapté la procédure pour queΔ=330ρ¯Δ=330ρ¯, alors que dans le cas des réseaux cérébraux, nous avons adapté les valeurs de ΔΔ de sorte que le rayon des nœuds dans les réseaux corresponde raisonnablement à la taille suggérée par l'inspection visuelle.
Nous avons ensuite construit la matrice de nœuds adjacente, MijMij, c'est-à-dire une matrice avec des lignes / colonnes égales au nombre de nœuds détectés, avec valeur Mij=1Mij=1 si les nœuds sont séparés par une distance ≤llink≤llink, ou Mij=0Mij=0autrement. Le choix dellinkllink est arbitraire, mais une analyse complète des paramètres réseau en fonction de llinkllinkest au-delà des objectifs de ce premier travail exploratoire. Nous nous sommes donc concentrés sur un choix spécifique pour la longueur de liaison, motivé par l'analyse récente des galaxies observées par de Regt et al. [ 33 ], qui a suggéréllink=1.2 Mpcllink=1.2 Mpc comme «longueur de liaison» de référence pour les halos de matière dans le réseau cosmique (c.-à-d. ∼L/100∼L/100sur la figure 2 ). Sur la base de la similitude des spectres de puissance après avoir renormalisé opportunément les échelles spatiales présentées dans la section 3.3, nous avons donc systématiquement redimensionné la longueur de liaison dans40×40× échantillons de cerveau à llink=16 μmllink=16 μm. La figure 3 donne une vue rapprochée des nœuds et des réseaux reconstruits pour trois tranches de notre ensemble de données.
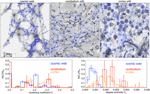
FIGURE 3 . Panneaux du haut: détails agrandis des connexions reconstruites entre les nœuds pour trois exemples de réseaux de notre échantillon (lignes bleues, superposées aux cartes de contraste de densité). Panneaux du bas: distributions du coefficient de regroupement et du degré de centralité pour toutes les tranches (les barres d'erreur donnent la dispersion au sein de chaque échantillon de tranches étudié). Les connexions reconstruites ne prennent pas en compte les connexions neuronales à longue portée et les clusters représentés sont purement spatiaux.
Cette méthode sélectionne parmi N∼3800−4700N∼3800−4700 nœuds dans nos tranches de toile cosmique, avec un nombre moyen de ⟨k⟩∼3.8−4.1⟨k⟩∼3.8−4.1connexions par nœud. Pour les tranches de cervelet, nous avons mesuré⟨k⟩∼1.9−3.7⟨k⟩∼1.9−3.7, tandis que pour le cortex nous avons mesuré ⟨k⟩∼4.6−5.4⟨k⟩∼4.6−5.4 pour le N∼1800−2000N∼1800−2000nœuds identifiés. D'autre part, le nombre moyen estimé de nœuds pour le web cosmique simulé est∼40%∼40%plus petit des résultats rapportés à partir des études de galaxies réelles par de Regt et al. [ 33 ], ce qui est compris en raison de l'épaisseur beaucoup plus petite de nos tranches de modèle (un facteur∼4∼4 plus mince en profondeur par rapport aux observations).
Les deux statistiques montrent clairement que le cerveau et les réseaux web cosmiques sont très différents des réseaux aléatoires Erdös – Rényi de même taille, qui prédiraient plutôt pour les deux paramètres Crandom≈⟨k⟩/NCrandom≈⟨k⟩/N (≤2⋅10−3≤2⋅10−3 dans notre cas) et Cd,random≈Crandom(1−Crandom)/NCd,random≈Crandom(1−Crandom)/N (≤10−7−10−6≤10−7−10−6dans notre cas), dans la limite d'un grand N [par exemple, Réf. 39 ]. Nous pouvons voir qu'au lieu de cela, toutes les distributions mesurées de C mesurent quelques pics différents dans leC∼0.1−0.4C∼0.1−0.4gamme, indiquant clairement que tous les réseaux sont fortement corrélés, c'est-à-dire que leurs liens ont tendance à être fortement regroupés. Dans le cas du réseau cosmique, des pics clairsemés similaires ont été mesurés en données réelles par de Regt et al. [ 33 ], et sont attribués aux galaxies en modéré (C∼0.1C∼0.1) ou riche (C∼0.3C∼0.3), comme des filaments ou de grands amas de galaxies. Seule la partie résiduelle des distributions, avecC≤10−2C≤10−2, marque à la place les régions du réseau dans lesquelles la connectivité est proche du hasard (par exemple, des nœuds dans des régions vides). Les réseaux ont également des valeurs de degré de centralité nettement plus importantes (de trois à quatre ordres de grandeur) que les réseaux aléatoires correspondants. Dans le réseau cosmique, les distributions deCdCdsont approximativement poissoniennes et en ligne avec le réseau de galaxies étudié par la Réf. 33 , même si les pics de la distribution sont à des valeurs inférieures à celles des échantillons de cerveau. Ce dernier est compatible avec la présence accrue de petits neurones dans la couche granulaire, déjà évoquée ci-dessus, qui conduit à la présence d'amas de nœuds plus serrés.
Nous soulignons que dans cette étude nous n'avons analysé qu'une fraction du cortex, et non l'ensemble du système nerveux central, dont l'architecture est évidemment différente. En fait, alors que la proximité peut décrire avec précision le réseau cosmique, les réseaux neuronaux sont basés sur des connexions et notre analyse n'est donc pas sensible à la connectivité à longue portée. Mais en effet, la connectivité à longue portée est connue pour être une caractéristique cruciale des réseaux neuronaux. Nous différons l'application de statistiques de réseau plus complexes [par exemple, Réf. 40 ]) aux travaux futurs.
Discussion
Nous avons présenté une comparaison détaillée entre le réseau neuronal et le web cosmique, deux des réseaux les plus fascinants et complexes de la Nature, dans le but d'évaluer le niveau de similitude entre ces deux systèmes physiques de manière objective.
Nous avons également appliqué des approches statistiques homogènes à des échantillons de laboratoire réels du cerveau et du cortex cérébelleux (section 2.1), et à des tranches de la distribution simulée de la matière noire et ordinaire dans le réseau cosmique (section 2.2), et quantifié leur morphologie et propriétés de réseau utilisant l'analyse spectrale (section 3.3) ainsi que les paramètres de réseau de la théorie des graphes (section 3.4). Dans la gamme d'hypothèses simplificatrices que nous avons utilisées pour définir les deux réseaux (par exemple, sur la base de la proximité des nœuds identifiés à partir de la distribution continue de matière rendue par différentes techniques d'imagerie), nos résultats suggèrent que des configurations de réseau similaires peuvent émerger de l'interaction de différents processus physiques, entraînant des niveaux similaires de complexité et d'auto-organisation,∼1027∼1027) de ces deux systèmes.
Nous sommes conscients que cette approche présente plusieurs limites. Premièrement, notre comparaison s'est concentrée sur la densité de la matière. La sélection des neurofilaments pour délimiter le réseau neuronal reposait sur le fait qu'ils sont exprimés assez uniformément dans le compartiment cytoplasmique des neurones. Nos résultats devraient être davantage validés avec différents marqueurs, comme des microfilaments ou des microtubules. Deuxièmement, nous avons supposé que la densité de coloration la plus élevée se situait au niveau du Soma neuronal, ce qui est une approximation conduisant à une définition non standard des nœuds. D'autres études sont nécessaires pour valider nos résultats avec des données de réseau neuronal fonctionnel et sans perdre la définition anatomo-visuelle. Troisièmement, notre étude s'est basée sur des coupes histologiques, qui ne peuvent évidemment montrer qu'une infime partie du réseau cérébral lui-même. En outre, alors que le web cosmique utilise la proximité pour définir son réseau, les réseaux de neurones sont basés sur des connexions qui peuvent être spatialement à grande distance et qui n'ont pas pu être correctement évaluées par notre analyse en raison des limites techniques de la méthode. Pour les limitations ci-dessus, nous n'avons pas pu présenter une analyse systématique et complète de la connectivité des réseaux, car nous nous sommes concentrés sur la simple proximité et non sur la connectivité longue portée. Une frontière clé de cette ligne de recherche comparative est la possibilité de mesurer la capacité de mémoire des deux réseaux, une tâche actuellement rendue difficile par les approches radicalement différentes actuellement disponibles pour mesurer et surveiller le flux d'informations en leur sein. Un fait intéressant illustre bien que des similitudes possibles existent également à cet égard.∼4.7∼4.7bits d'information par cellule neuronale [ 41 ]. Extrapolé au nombre moyen total de nœuds dans le réseau neuronal, cela donne≈2⋅1016 bits≈2⋅1016 bits, c'est à dire, ∼2.5∼2.5Pétaoctets comme capacité de mémoire du cerveau humain. Pour le web cosmique, une idée radicalement différente basée sur la théorie de l'information peut être utilisée pour quantifier la quantité d'informations codées par la structure tridimensionnelle du web cosmique [ 42 , 43 ]. A travers le calcul de la «complexité statistique» qui caractérise l'évolution dynamique des univers simulés, on a fait valoir que∼3.5⋅1016∼3.5⋅1016 bits (c'est-à-dire, ≈4.3≈4.3 Pétaoctets de mémoire) sont nécessaires pour stocker les informations de la structure cosmique dans tout l'Univers observable (≈13.8 Gpc≈13.8 Gpc). Une telle concordance peut apparaître comme une simple coïncidence, étant donné que, compte tenu des ambiguïtés dans la définition des deux réseaux, en particulier du réseau cosmique, ces chiffres ne sont connus qu'approximativement.
Avec le reste de l'analyse présentée dans ce travail, ces similitudes sont destinées à motiver le développement d'algorithmes plus puissants et plus discriminants pour identifier les analogies et les différences de ces systèmes fascinants, presque aux extrêmes imaginables des échelles spatiales dans l'Univers.
Déclaration de disponibilité des données
Tous les échantillons de cerveau analysés dans ce travail, ainsi que les échantillons pertinents du web cosmique simulé et de la connectivité réseau reconstruite sont accessibles au public à cette URL: https://cosmosimfrazza.myfreesites.net/cosmic-web-and-brain-network- ensembles de données .
Déclaration d'éthique
Cette étude a été réalisée conformément aux recommandations de l'hôpital universitaire de Modène. Tous les sujets ont donné leur consentement éclairé écrit conformément à la Déclaration d'Helsinki.
Les contributions de l'auteur
Les deux auteurs ont contribué à la rédaction du manuscrit et à l'interprétation des résultats. FV est responsable de la production des simulations cosmologiques et des méthodes numériques adoptées dans l'article. L'AF est responsable de l'extraction des échantillons de cerveau utilisés dans ce travail.
Financement
FV reconnaît le soutien financier de la subvention de démarrage ERC «MAGCOW», no. 714196.
Conflit d'intérêt
Les auteurs déclarent que la recherche a été menée en l'absence de toute relation commerciale ou financière pouvant être interprétée comme un conflit d'intérêts potentiel.
Remerciements
Nous remercions chaleureusement Elena Zunarelli (Département de Pathologie Anatomique, Hôpital Universitaire Policlinico di Modena, Modène, Italie) pour la production des tranches utilisées dans la Figure 1 . La simulation cosmologique de ces travaux a été réalisée à l'aide du code ENZO ( http://enzo-project.org ), qui est le produit d'un effort collaboratif de scientifiques de nombreuses universités et laboratoires nationaux. Les simulations / analyses de ce travail ont été réalisées sur le supercalculateur Piz Daint au CSCS-ETHZ (Lugano, Suisse) et sur Marconi au CINECA (Bologne, Italie) dans le cadre des projets s805 et INA17_C4A28 avec (FV comme chercheur principal). FV reconnaît l'utilisation des outils de stockage en ligne aimablement fournis par l'initiave INAF Astronomical Archive (IA2) ( http://www.ia2.inaf.it)). Nous remercions vivement la lecture attentive de ce manuscrit de D. Wittor.
1. Sporns O. Le connectome humain: un réseau complexe. Ann NY Acad Sci. (2011). 1224 : 109–25. doi: 10.1111 / j.1749-6632.2010.05888.x






 F. Vazza
F. Vazza 


